![]() Top: 5 lines / syttrea
Top: 5 lines / syttrea
![]() Par: 9 lines
Par: 9 lines
$lm0, $lm2, ..., $lm38 に格納された \(20\) 個の Long に \(2\) を加えた結果をそれぞれ $ln0, $ln2, ..., $ln38 へ出力してください。
今回は Int(\(32\) bit 整数)ではなく Long(\(64\) bit 整数)を扱う問題になります。
したがって、iinc の代わりに linc を利用しましょう。
linc を \(2\) 回使えば良さそうですが、以下のように中間結果を $lm100v に置こうとすると、エラーになってしまいます。
これは、次の \(2\) つの制約に引っかかっています。
例えば以下のように使用するアドレスを変更した上で、さらに間を \(2\) ステップ空ければ実行できます。
この調子で \(5\) 回繰り返せば \(20\) 行で Accepted できますが、何もしない no operation 命令 nop がもったいないところです。
PE には LM のほかに GRF (General Register File) という記憶領域が \(2\) つ、GRF0 と GRF1 があり、それぞれ \(256\) 長語の容量があります。
アクセス方法は LM と同様で、GRF0 は $r で、GRF1 は $s で、長語も同じく $lr, $ls でアクセスします。GRF の「R」と、その次のアルファベット「S」と覚えてください。
容量が小さい代わりに次の特長があります。
linc $lr0v $lr100v)GRF を使用すれば、以下のように nop を少なくできます。
\(0\) サイクル目から順に $lr0, $lr2, $lr4, $lr6 に書き込みを行います。次の \(4\) サイクルは何も行わず、その後 $lr0, $lr2, $lr4, $lr6 から読み出しを行います。
$lr0 に注目すると書き込み指示を行ってから \(8\) サイクル後に読み出しを行っているため、制約に違反しません。
さらに LM と異なり、GRF は連続で読み書きできます。以下の例では nop の代わりに別の linc を行うことで、\(4\) 命令で \(8\) 長語を処理しています。
実は、inc などを計算させている ALU にはフォワーディングパス $aluf があります。
これを使うことによって、次のように直前の ALU 命令の出力を利用でき、GRF を使わずとも \(2\) 命令で \(4\) 要素を処理できます。
$nowrite とは、どのレジスタにも書き込まない事を意味します。どこにも書き込まなくても $aluf には出力されます。
次のステップ以外でも計算結果を使用したい場合はレジスタに書き込み、次のステップでは $aluf から参照するということもできます。
$lr0v に書き込んだにも関わらず、その後使用しないことも無駄ですが動作します。デバッグなどで有用です。
linc を \(2\) 回使用し、\(5\) セット行えば \(10\) 行で Accepted できます。
しかし、即値命令で定数 \(2\) を作り、加算命令で加算をすることでもっと短くなります。
Short や Half)を指示した場合、繰り返されて \(32\) bit になりますLong や Double)は生成できません例えば以下のように使用します。
Int (\(32\) bit 値) を 長語 (\(64\) bit) に書き込むと、\(2\) 回繰り返された値が毎サイクル書き込まれます。
詳しく挙動を知りたい方には、d get によるメモリダンプデバッグが役に立ちます。
さて、今回は Long (\(64\) bit値) に \(2\) を加える問題でした。しかし、以下のように書いてもうまくいきません。
結果:
即値命令は \(32\) bit の値しか受け取れず、長語 (\(64\) bit) に書き込むと繰り返されるためです。
つまり、i"2" = 0x00000002 を繰り返した 0x0000000200000002 = \(8589934594\) が $lr0v に書き込まれます。
これを長語加算 ladd した結果、\(2\) ではなく \(8589934594\) が加算されてしまっていたのです。
\(64\) bit 値を生成するには、imm 命令を \(2\) 回使う必要があります。
これで、最初の \(4\) つの Long に \(2\) を加えることができました。省略した残りの \(4\) 行を完成させることで、\(9\) 命令で Accepted できます。
しかし、先程は \(1\) 個で良かった nop の数が \(2\) つに増えてしまいました。\(1\) 個だとエラーです。
imm i"2" $r1 を考えると、\(4\) サイクル全てで $r1 に書き込んでいます。
nop が \(1\) つの場合、ladd $lm0v $lr0 で $r1 を使用すると、最後に書き込んでから間に \(4\) サイクルしかありません。
そのため GRF の「書き込みから \(7\) サイクル後から読み出せる」というルールに違反しているので、この例の書き方ではもっと nop が必要になるのです。
nop の数を削るなどして工夫をすると、より少ない行数で Accepted できます。ぜひ目指してみましょう。
さて、ここで ALU の語長の指定について改めて解説しましょう。ALU などの演算器は iadd の i などの演算の精度指定と、$lr0 の l などの入出力の語長の指定は独立しています。
入出力のオペランドには 単語、長語、\(2\) 長語(例: $r0、$lr0、$llr0)の \(3\) 種類の語長が指定できます。
\(2\) 長語は \(128\) bit の領域を表し、LM, GRF へのアクセスでは接頭辞 ll を使用します。$llr0 の次に有効な場所は $llr4 になります。
ALU では即値命令 imm や、コピー命令 passa、一部の変換命令は \(2\) 長語を扱うことができます。
演算器には常に \(2\) 長語が入力されます。短い語長が指定された場合、末尾に \(0\) が埋められて入力されます。
次に演算としての精度の指定です。例えば足し算をする命令として ladd, iadd, sadd の \(3\) つがありますが、これは各サイクルで入力される \(2\) 長語のうち、先頭 \(64\) bit の \(1\) 長語をどう区切って計算するか、だけに影響します。
最後に、演算器は常に \(2\) 長語を出力しており、出力先の語長に合わせて先頭部の値が書き込まれます。
$aluf は、この \(2\) 長語の出力を記録しており、次のステップで使用する際は常に \(2\) 長語の入力として扱われます。
いくつかの命令の様子を図示すると以下のようになります。

sinc $lm0 $ln0 のように、入力と出力の語長が同じであれば特に意識することなく使用できますが、$aluf を使用した際など、前の命令の語長と次の命令の語長が異なる場合などは注意が必要です。
これらの仕様から、単語を入力として、長語インクリメントを行い、\(2\) 長語へ書き込みをする
も、命令としては有効です。

このとき、\(2\) 長語動作する命令以外(inc, add など大半の演算命令)では、ALU が出力する値の末尾 \(1\) 長語は、第 \(1\) 入力の末尾そのままとなっています。(SDM 3.6.12「ALU 命令式」)
そのためこの例では、入力の $m0 (\(32\) bit) を \(a\) とすると、出力の $lln0 (\(128\) bit) へは \(a\times 2^{96} + 2^{64}\) (\(32\) bit 値 × \(4\) 個だと考えると \(\{a, 1, 0, 0\}\))が書き込まれます。
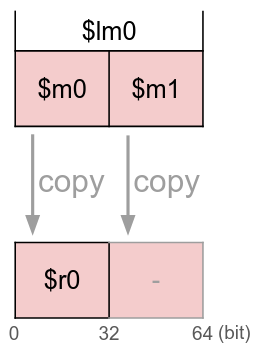
次に、長語(\(64\) bit)$lm0 を単語(\(32\) bit)$r0 へコピーする以下の VSM をご覧ください。
このとき、リトルエンディアンな環境に慣れていると $r0 には $lm0 の下位 \(32\) bit が書き込まれると期待することでしょう。
しかし、上記のルールから、$r0 には $lm0 の上位 \(32\) bit が各サイクルで書き込まれます。
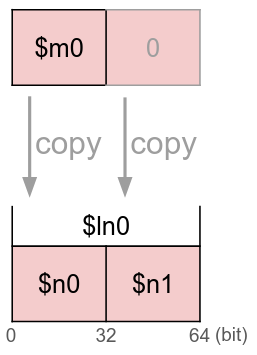
次は逆に、単語を長語に書き込む例です。
この時、出力 $ln0 の \(64\) bit のうち、上位 \(32\) bit に $m0 の値が、下位 \(32\) bit に \(0\) が書き込まれます。
MN-Core プログラミングの際は、このようなビッグエンディアン動作にお気をつけください。
$r1 と記述すると毎サイクル $r1 へ書き込まれてしまうので、$r1v や、 $r[1,100,100,100] などで最初のサイクルだけ $r1 に書き込むようにします。
$r0v は入力部分以外なので最初から \(0\) で初期化されているため、 imm i"0" $r0v は必要ありません。
愚直に nop を削り、$aluf を使う以下の方法では、\(2\) ではなく 0x200000002 = 8589934594 が加算されてしまいます。
これは、GRF への書き込みは単語で行われていますが、$aluf は ALU の出力がそのまま記録されるからです。
ここで、問題の Inputs を見ると、\(0 \le X[i] \le 99\) と書かれています。
つまり、値の型としては Long ですが、今回は Int の加算で十分です。
出力の LM1 の領域は \(0\) で初期化されているため、Long の下 \(32\) bit である $m1 に \(2\) を加算し、$n1 に出力すれば良いです。
ただし、
ladd $m1v $aluf $n1v と書いても、\(2\) 要素目以降がずれてしまいます。Long の下 \(32\) bitだけ作用させたいからです。
ladd $m[1,3,5,7] $aluf $n[1,3,5,7] もしくは増分を指定する Auto Stride 表記で ladd $m1v2 $aluf $n1v2 とすることで、\(6\) 行で正解できます。
\(6\) 行解法までは制約などを活用した解法でした。
本コンテストはテストケースが公開されているため、これに着目した入力依存の解法が、この問題には存在します。
練習問題は MN-Core の動作について順を追って理解していただくために、Plus 2 までは複数 PE ではなく単 PE 用のテストケースで用意されています。
\(3\) 問目の A+B 以降は複数 PE を利用する強固なテストになるように作成されているため、テストケースの内容依存で短くする解法は無いと考えています。
テストケースは、問題ページの Testcases からダウンロードできます。またコードテストを実行した際に出力される inputs からも確認できます。
入力と正解出力は以下のとおりです。
inputs: [12, 0, 25, 61, 28, 49, 67, 95, 92, 86, 76, 79, 52, 99, 64, 73, 83, 89, 57, 70]
expect: [14, 2, 27, 63, 30, 51, 69, 97, 94, 88, 78, 81, 54,101, 66, 75, 85, 91, 59, 72]
どうにかして \(5\) 行で解けないでしょうか。
正攻法で「\(2\) を足す」方法では実現不可能です。
$m[314,15,926,53] のような、\(4\) サイクルで自由にアドレスを指定できる MN-Core 2 の特徴を使用します。
入出力をソートして、観察してみましょう
inputs: [0, 12, 25, 28, 49, 52, 57, 61, 64, 67, 70, 73, 76, 79, 83, 86, 89, 92, 95, 99]
expect: [2, 14, 27, 30, 51, 54, 59, 63, 66, 69, 72, 75, 78, 81, 85, 88, 91, 94, 97, 101]
MN-Core は、以下のように出力先を複数指定することが可能であり、同じ値が書き込まれます。
入力を観察していると、例えば \(64\) を dec すると \(63\) が作れそうです。
dec だけでは expect の値は作れないので、他の演算も使います。
LM0 にある入力の値と GRF に置いた出力の値で xor して他の出力が作れないか探索してみると、以下のようにできることがわかります。
途中で \(2\) が生成されるので、最後は ladd を使っていますが、dec と xor だけでもできるようです。
他にも、add や sub を使って作ることができます。
興味があればぜひ他の解法も探索してみてください。
「\(6\) 行解法」において、入力依存解法として適当な 2 要素の差などで Long の \(2\) が作れると、単語書き込みを行わなくても \(6\) 行で正解できます。
そのため、inc, dec, add, sub, and, xor, shift, bshift, msb1 >> x, などで \(2\) が作れないようにテストケースは作成されています。
ただし、練習問題であるため、入力の値域は大きくしすぎるとデバッグがしにくいため、 \(0\) から \(99\) までの値域に収めています。
その結果、値の探索を行う入力依存解法を防ぐのは困難でした。
入力依存解法が正解法よりも短くなる事は無いようにテストケースは作成しており、本問題も複数 PE を使用するテストケースにすることで防ぐことは可能でしたが、
・Plus 2 までは PE が複数あることを説明していない
・練習問題は行数によらず一律 \(10\) 点
・練習問題は解法共有可
・\(5\) 行解法を考えつくのも難しく、方針を思いついた後も手を動かす必要がある
ということを踏まえ、入力依存解法が存在する問題として出題しました。
お楽しみいただけたでしょうか。
$lm[0:40], /((20:1); B@[PE,MAB,L1B,L2B])
$ln[0:40], /((20:1))